Fully coupled poroelastic problem¶
This system may be downloaded from the CoupCons3D page (use the Matrix Market download option). According to the description, the system has been obtained through a Finite Element transient simulation of a fully coupled consolidation problem on a three-dimensional domain using Finite Differences for the discretization in time. More details available in [FePG09] and [FeJP12]. The RHS vector for the CoupCons3D problem is not provided, and we use the RHS vector filled with ones.
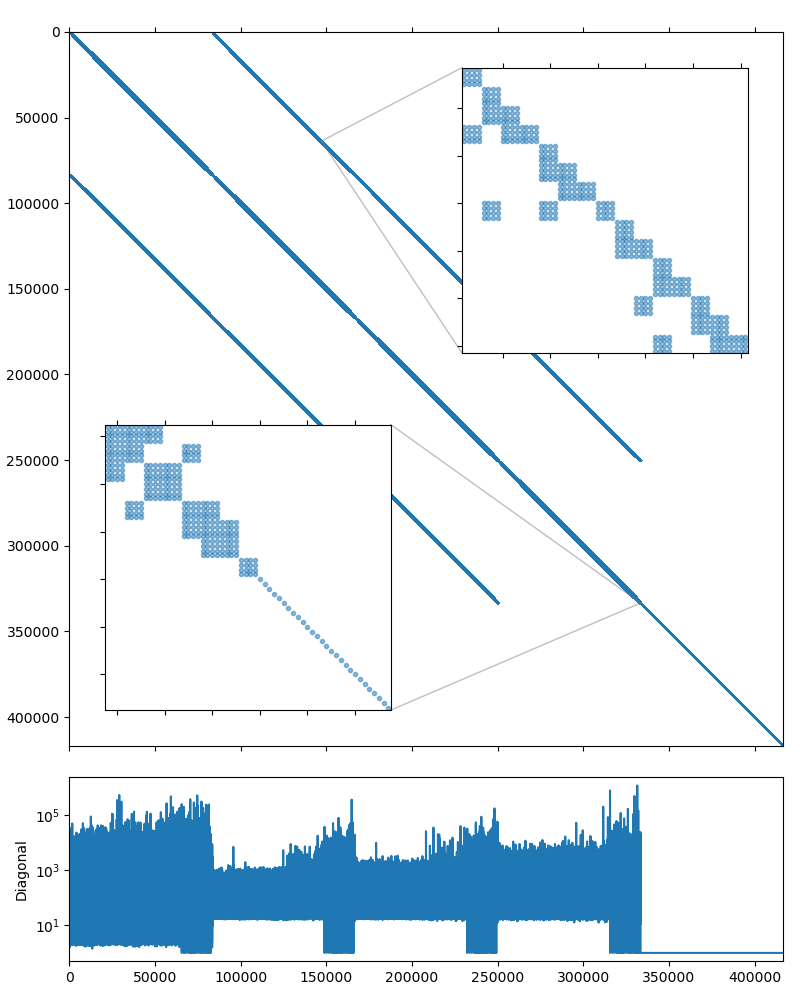
The system matrix is non-symmetric and has 416,800 rows and 17,277,420 nonzero values, which corresponds to an average of 41 nonzeros per row. The matrix portrait is shown on the figure below.
| [FePG09] |
|
| [FeJP12] |
|
Once again, lets start our experiments with the examples/solver utility after converting the matrix into binary format with examples/mm2bin. The default options do not seem to work for this problem:
$ solver -B -A CoupCons3D.bin
Solver
======
Type: BiCGStab
Unknowns: 416800
Memory footprint: 22.26 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.11
Grid complexity: 1.09
Memory footprint: 447.17 M
level unknowns nonzeros memory
---------------------------------------------
0 416800 22322336 404.08 M (90.13%)
1 32140 2214998 38.49 M ( 8.94%)
2 3762 206242 3.58 M ( 0.83%)
3 522 22424 1.03 M ( 0.09%)
Iterations: 100
Error: 0.705403
[Profile: 16.981 s] (100.00%)
[ reading: 0.187 s] ( 1.10%)
[ setup: 0.584 s] ( 3.44%)
[ solve: 16.209 s] ( 95.45%)
What seems to works is using the higher quality relaxation (incomplete LU decomposition with zero fill-in):
$ solver -B -A CoupCons3D.bin precond.relax.type=ilu0
Solver
======
Type: BiCGStab
Unknowns: 416800
Memory footprint: 22.26 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.11
Grid complexity: 1.09
Memory footprint: 832.12 M
level unknowns nonzeros memory
---------------------------------------------
0 416800 22322336 751.33 M (90.13%)
1 32140 2214998 72.91 M ( 8.94%)
2 3762 206242 6.85 M ( 0.83%)
3 522 22424 1.03 M ( 0.09%)
Iterations: 47
Error: 4.8263e-09
[Profile: 13.664 s] (100.00%)
[ reading: 0.188 s] ( 1.38%)
[ setup: 1.708 s] ( 12.50%)
[ solve: 11.765 s] ( 86.11%)
From the matrix diagonal plot in CoupCons3D matrix portrait it is clear that the system, as in Structural problem case, has high contrast coefficients. Scaling the matrix so it has the unit diagonal should help here as well:
$ solver -B -A CoupCons3D.bin precond.relax.type=ilu0 -s
Solver
======
Type: BiCGStab
Unknowns: 416800
Memory footprint: 22.26 M
Preconditioner
==============
Number of levels: 3
Operator complexity: 1.10
Grid complexity: 1.08
Memory footprint: 834.51 M
level unknowns nonzeros memory
---------------------------------------------
0 416800 22322336 751.33 M (90.54%)
1 32140 2214998 73.06 M ( 8.98%)
2 2221 116339 10.12 M ( 0.47%)
Iterations: 11
Error: 9.79966e-09
[Profile: 4.826 s] (100.00%)
[ self: 0.064 s] ( 1.34%)
[ reading: 0.188 s] ( 3.90%)
[ setup: 1.885 s] ( 39.06%)
[ solve: 2.689 s] ( 55.71%)
Another thing to note from the CoupCons3D matrix portrait is that the system matrix has block structure, with two diagonal subblocks. The upper left subblock contains 333,440 unknowns and seems to have a block structure of its own with small \(4\times4\) blocks, and the lower right subblock is a simple diagonal matrix with 83,360 unknowns. Fortunately, 83,360 is divisible by 4, so we should be able to treat the whole system as if it had \(4\times4\) block structure:
$ solver -B -A CoupCons3D.bin precond.relax.type=ilu0 -s -b4
Solver
======
Type: BiCGStab
Unknowns: 104200
Memory footprint: 22.26 M
Preconditioner
==============
Number of levels: 3
Operator complexity: 1.18
Grid complexity: 1.11
Memory footprint: 525.68 M
level unknowns nonzeros memory
---------------------------------------------
0 104200 1395146 445.04 M (84.98%)
1 10365 235821 70.07 M (14.36%)
2 600 10792 10.57 M ( 0.66%)
Iterations: 4
Error: 2.90461e-09
[Profile: 1.356 s] (100.00%)
[ self: 0.063 s] ( 4.62%)
[ reading: 0.188 s] ( 13.84%)
[ setup: 0.478 s] ( 35.23%)
[ solve: 0.628 s] ( 46.30%)
This is much better! Looks like switching to the block-valued backend not only improved the setup and solution performance, but also increased the convergence speed. This version is about 12 times faster than the first working approach. Lets see how this translates to the code, with the added bonus of using the mixed precision solution. The source below shows the complete solution and is also available in tutorial/3.CoupCons3D/coupcons3d.cpp. The only differences (highlighted in the listing) with the solution from Structural problem are the choices of the iterative solver and the smoother, and the block size.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 | #include <vector>
#include <iostream>
#include <amgcl/backend/builtin.hpp>
#include <amgcl/adapter/crs_tuple.hpp>
#include <amgcl/make_solver.hpp>
#include <amgcl/amg.hpp>
#include <amgcl/coarsening/smoothed_aggregation.hpp>
#include <amgcl/relaxation/ilu0.hpp>
#include <amgcl/solver/bicgstab.hpp>
#include <amgcl/value_type/static_matrix.hpp>
#include <amgcl/adapter/block_matrix.hpp>
#include <amgcl/io/mm.hpp>
#include <amgcl/profiler.hpp>
int main(int argc, char *argv[]) {
// The command line should contain the matrix file name:
if (argc < 2) {
std::cerr << "Usage: " << argv[0] << " <matrix.mtx>" << std::endl;
return 1;
}
// The profiler:
amgcl::profiler<> prof("Serena");
// Read the system matrix:
ptrdiff_t rows, cols;
std::vector<ptrdiff_t> ptr, col;
std::vector<double> val;
prof.tic("read");
std::tie(rows, cols) = amgcl::io::mm_reader(argv[1])(ptr, col, val);
std::cout << "Matrix " << argv[1] << ": " << rows << "x" << cols << std::endl;
prof.toc("read");
// The RHS is filled with ones:
std::vector<double> f(rows, 1.0);
// Scale the matrix so that it has the unit diagonal.
// First, find the diagonal values:
std::vector<double> D(rows, 1.0);
for(ptrdiff_t i = 0; i < rows; ++i) {
for(ptrdiff_t j = ptr[i], e = ptr[i+1]; j < e; ++j) {
if (col[j] == i) {
D[i] = 1 / sqrt(val[j]);
break;
}
}
}
// Then, apply the scaling in-place:
for(ptrdiff_t i = 0; i < rows; ++i) {
for(ptrdiff_t j = ptr[i], e = ptr[i+1]; j < e; ++j) {
val[j] *= D[i] * D[col[j]];
}
f[i] *= D[i];
}
// We use the tuple of CRS arrays to represent the system matrix.
// Note that std::tie creates a tuple of references, so no data is actually
// copied here:
auto A = std::tie(rows, ptr, col, val);
// Compose the solver type
typedef amgcl::static_matrix<double, 4, 4> dmat_type; // matrix value type in double precision
typedef amgcl::static_matrix<double, 4, 1> dvec_type; // the corresponding vector value type
typedef amgcl::static_matrix<float, 4, 4> smat_type; // matrix value type in single precision
typedef amgcl::backend::builtin<dmat_type> SBackend; // the solver backend
typedef amgcl::backend::builtin<smat_type> PBackend; // the preconditioner backend
typedef amgcl::make_solver<
amgcl::amg<
PBackend,
amgcl::coarsening::smoothed_aggregation,
amgcl::relaxation::ilu0
>,
amgcl::solver::bicgstab<SBackend>
> Solver;
// Initialize the solver with the system matrix.
// Use the block_matrix adapter to convert the matrix into
// the block format on the fly:
prof.tic("setup");
auto Ab = amgcl::adapter::block_matrix<dmat_type>(A);
Solver solve(Ab);
prof.toc("setup");
// Show the mini-report on the constructed solver:
std::cout << solve << std::endl;
// Solve the system with the zero initial approximation:
int iters;
double error;
std::vector<double> x(rows, 0.0);
// Reinterpret both the RHS and the solution vectors as block-valued:
auto f_ptr = reinterpret_cast<dvec_type*>(f.data());
auto x_ptr = reinterpret_cast<dvec_type*>(x.data());
auto F = amgcl::make_iterator_range(f_ptr, f_ptr + rows / 4);
auto X = amgcl::make_iterator_range(x_ptr, x_ptr + rows / 4);
prof.tic("solve");
std::tie(iters, error) = solve(Ab, F, X);
prof.toc("solve");
// Output the number of iterations, the relative error,
// and the profiling data:
std::cout << "Iters: " << iters << std::endl
<< "Error: " << error << std::endl
<< prof << std::endl;
}
|
The output from the compiled program is given below. The main improvement here is the reduced memory footprint of the single-precision preconditioner: it takes 279.83M as opposed to 525.68M in the full precision case. The setup and the solution are slightly faster as well:
$ ./coupcons3d CoupCons3D.mtx
Matrix CoupCons3D.mtx: 416800x416800
Solver
======
Type: BiCGStab
Unknowns: 104200
Memory footprint: 22.26 M
Preconditioner
==============
Number of levels: 3
Operator complexity: 1.18
Grid complexity: 1.11
Memory footprint: 279.83 M
level unknowns nonzeros memory
---------------------------------------------
0 104200 1395146 237.27 M (84.98%)
1 10365 235821 37.27 M (14.36%)
2 600 10792 5.29 M ( 0.66%)
Iters: 4
Error: 2.90462e-09
[Serena: 14.415 s] (100.00%)
[ self: 0.057 s] ( 0.39%)
[ read: 13.426 s] ( 93.14%)
[ setup: 0.345 s] ( 2.39%)
[ solve: 0.588 s] ( 4.08%)
We can also use the VexCL backend to accelerate the solution using the GPU. Again, this is very close to the approach described in Structural problem (see tutorial/3.CoupCons3D/coupcons3d_vexcl.cpp). However, the ILU(0) relaxation is an intrinsically serial algorithm, and is not effective with the fine grained parallelism of the GPU. Instead, the solutions of the lower and upper parts of the incomplete LU decomposition in AMGCL are approximated with several Jacobi iterations [ChPa15]. This makes the relaxation relatively more expensive than on the CPU, and the speedup from using the GPU backend is not as prominent:
$ ./coupcons3d_vexcl_cuda CoupCons3D.mtx
1. GeForce GTX 1050 Ti
Matrix CoupCons3D.mtx: 416800x416800
Solver
======
Type: BiCGStab
Unknowns: 104200
Memory footprint: 22.26 M
Preconditioner
==============
Number of levels: 3
Operator complexity: 1.18
Grid complexity: 1.11
Memory footprint: 281.49 M
level unknowns nonzeros memory
---------------------------------------------
0 104200 1395146 238.79 M (84.98%)
1 10365 235821 37.40 M (14.36%)
2 600 10792 5.31 M ( 0.66%)
Iters: 5
Error: 6.30647e-09
[Serena: 14.432 s] (100.00%)
[ self: 0.060 s] ( 0.41%)
[ GPU matrix: 0.213 s] ( 1.47%)
[ read: 13.381 s] ( 92.72%)
[ setup: 0.549 s] ( 3.81%)
[ solve: 0.229 s] ( 1.59%)
Note
We used the fact that the matrix size is divisible by 4 in order to use the block-valued backend. If it was not the case, we could use the Schur pressure correction preconditioner to split the matrix into two large subsystems, and use the block-valued solver for the upper left subsystem. See an example of such a solution in tutorial/3.CoupCons3D/coupcons3d_spc.cpp. The performance is worse than what we were able to achive above, but still is better than the first working version:
$ ./coupcons3d_spc CoupCons3D.mtx 333440
Matrix CoupCons3D.mtx: 416800x416800
Solver
======
Type: BiCGStab
Unknowns: 416800
Memory footprint: 22.26 M
Preconditioner
==============
Schur complement (two-stage preconditioner)
Unknowns: 416800(83360)
Nonzeros: 22322336
Memory: 549.90 M
[ U ]
Solver
======
Type: PreOnly
Unknowns: 83360
Memory footprint: 0.00 B
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.21
Grid complexity: 1.23
Memory footprint: 206.09 M
level unknowns nonzeros memory
---------------------------------------------
0 83360 1082798 167.26 M (82.53%)
1 14473 184035 28.49 M (14.03%)
2 4105 39433 6.04 M ( 3.01%)
3 605 5761 4.30 M ( 0.44%)
[ P ]
Solver
======
Type: PreOnly
Unknowns: 83360
Memory footprint: 0.00 B
Preconditioner
==============
Relaxation as preconditioner
Unknowns: 83360
Nonzeros: 2332064
Memory: 27.64 M
Iters: 7
Error: 5.0602e-09
[CoupCons3D: 14.427 s] (100.00%)
[ read: 13.010 s] ( 90.18%)
[ setup: 0.336 s] ( 2.33%)
[ solve: 1.079 s] ( 7.48%)