Stokes-like problem¶
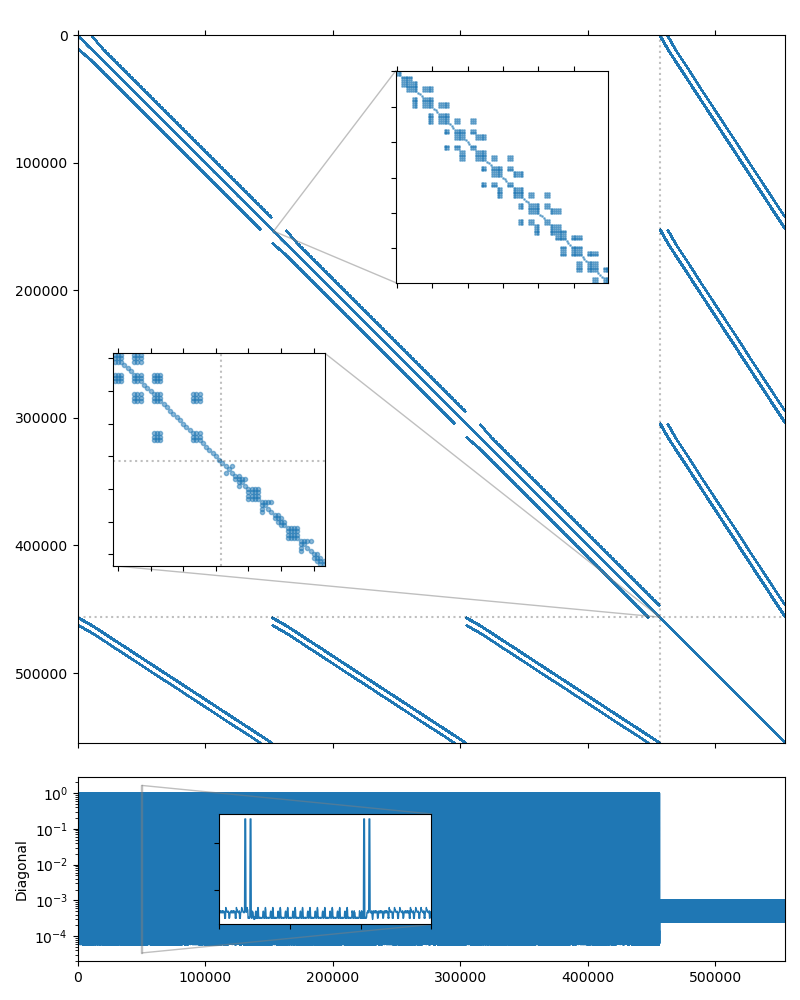
In this section we consider a saddle point system which was obtained by discretization of the steady incompressible Stokes flow equations in a unit cube with a locally divergence-free weak Galerkin finite element method. The UCube(4) system studied here may be downloaded from the the dataset accompanying the paper [DeMW20]. We will use the UCube(4) system from the dataset. The system matrix is symmetric and has 554,496 rows and 14,292,884 nonzero values, which corresponds to an average of 26 nonzero entries per row. The matrix sparsity portrait is shown on the figure below.
As with any Stokes-like problem, the system has a general block-wise structure:
In this case, the upper left subblock \(A\) corresponds the the flow unknowns, and itself has block-wise structure with small \(3\times3\) blocks. The lower right subblock \(C\) corresponds to the pressure unknowns. There is a lot of research dedicated to the efficient solution of such systems, see [BeGL05] for an extensive overview. The direct approach of using a monolithic preconditioner usually does not work very well, but we may try it to have a reference point. The AMG preconditioning does not yield a converging solution, but a single level ILU(0) relaxation seems to work with a CG iterative solver:
$ solver -B -A ucube_4_A.bin -f ucube_4_b.bin \
solver.type=cg solver.maxiter=500 \
precond.class=relaxation precond.type=ilu0
Solver
======
Type: CG
Unknowns: 554496
Memory footprint: 16.92 M
Preconditioner
==============
Relaxation as preconditioner
Unknowns: 554496
Nonzeros: 14292884
Memory: 453.23 M
Iterations: 270
Error: 6.84763e-09
[Profile: 9.300 s] (100.00%)
[ reading: 0.133 s] ( 1.43%)
[ setup: 0.561 s] ( 6.03%)
[ solve: 8.599 s] ( 92.46%)
A preconditioner that takes the structure of the system into account should be a better choice performance-wise. AMGCL provides an implementation of the Schur complement pressure correction preconditioner. The preconditioning step consists of solving two linear systems:
Here \(S\) is the Schur complement \(S = C - B_2 A^{-1} B_1^T\). Note that forming the Schur complement matrix explicitly is prohibitively expensive, and the following approximation is used to create the preconditioner for the first equation in (2):
There is no need to solve the equations (2) exactly. It is enough to perform a single application of the corresponding preconditioner as an approximation to \(S^{-1}\) and \(A^{-1}\). This means that the overall preconditioner is linear, and we may use a non-flexible iterative solver with it. The approximation matrix \(\hat S\) has a simple band diagonal structure, and a diagonal SPAI(0) preconditioner should have reasonable performance.
Similar to the examples/solver, the examples/schur_pressure_correction
utility allows to play with the Schur pressure correction preconditioner
options before trying to write any code. We found that using the non-smoothed
aggregation with ILU(0) smoothing on each level for the flow subsystem
(usolver) and single-level SPAI(0) relaxation for the Schur complement
subsystem (psolver) works best. We also disable lumping of the diagonal of
the \(A\) matrix in the Schur complement approximation with the
precond.simplec_dia=false option, and enable block-valued backend for the
flow susbsystem with the --ub 3 option. The -m '>456192' option sets
the pressure mask pattern. It tells the solver that all unknowns starting with
the 456192-th belong to the pressure subsystem:
$ schur_pressure_correction -B -A ucube_4_A.bin -f ucube_4_b.bin -m '>456192' \
-p solver.type=cg solver.maxiter=200 \
precond.simplec_dia=false \
precond.usolver.solver.type=preonly \
precond.usolver.precond.coarsening.type=aggregation \
precond.usolver.precond.relax.type=ilu0 \
precond.psolver.solver.type=preonly \
precond.psolver.precond.class=relaxation \
--ub 3
Solver
======
Type: CG
Unknowns: 554496
Memory footprint: 16.92 M
Preconditioner
==============
Schur complement (two-stage preconditioner)
Unknowns: 554496(98304)
Nonzeros: 14292884
Memory: 587.45 M
[ U ]
Solver
======
Type: PreOnly
Unknowns: 152064
Memory footprint: 0.00 B
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.25
Grid complexity: 1.14
Memory footprint: 233.07 M
level unknowns nonzeros memory
---------------------------------------------
0 152064 982416 188.13 M (80.25%)
1 18654 197826 35.07 M (16.16%)
2 2619 35991 6.18 M ( 2.94%)
3 591 7953 3.69 M ( 0.65%)
[ P ]
Solver
======
Type: PreOnly
Unknowns: 98304
Memory footprint: 0.00 B
Preconditioner
==============
Relaxation as preconditioner
Unknowns: 98304
Nonzeros: 274472
Memory: 5.69 M
Iterations: 35
Error: 8.57921e-09
[Profile: 3.872 s] (100.00%)
[ reading: 0.131 s] ( 3.38%)
[ schur_complement: 3.741 s] ( 96.62%)
[ self: 0.031 s] ( 0.79%)
[ setup: 0.301 s] ( 7.78%)
[ solve: 3.409 s] ( 88.05%)
Lets see how this translates to the code. Below is the complete listing of the solver (tutorial/4.Stokes/stokes_ucube.cpp) which uses the mixed precision approach.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 | #include <iostream>
#include <string>
#include <amgcl/backend/builtin.hpp>
#include <amgcl/adapter/crs_tuple.hpp>
#include <amgcl/value_type/static_matrix.hpp>
#include <amgcl/adapter/block_matrix.hpp>
#include <amgcl/preconditioner/schur_pressure_correction.hpp>
#include <amgcl/make_solver.hpp>
#include <amgcl/make_block_solver.hpp>
#include <amgcl/amg.hpp>
#include <amgcl/solver/cg.hpp>
#include <amgcl/solver/preonly.hpp>
#include <amgcl/coarsening/aggregation.hpp>
#include <amgcl/relaxation/ilu0.hpp>
#include <amgcl/relaxation/spai0.hpp>
#include <amgcl/relaxation/as_preconditioner.hpp>
#include <amgcl/io/binary.hpp>
#include <amgcl/profiler.hpp>
//---------------------------------------------------------------------------
int main(int argc, char *argv[]) {
// The command line should contain the matrix and the RHS file names,
// and the number of unknowns in the flow subsytem:
if (argc < 4) {
std::cerr << "Usage: " << argv[0] << " <matrix.bin> <rhs.bin> <nu>" << std::endl;
return 1;
}
// The profiler:
amgcl::profiler<> prof("UCube4");
// Read the system matrix:
ptrdiff_t rows, cols;
std::vector<ptrdiff_t> ptr, col;
std::vector<double> val, rhs;
prof.tic("read");
amgcl::io::read_crs(argv[1], rows, ptr, col, val);
amgcl::io::read_dense(argv[2], rows, cols, rhs);
std::cout << "Matrix " << argv[1] << ": " << rows << "x" << rows << std::endl;
std::cout << "RHS " << argv[2] << ": " << rows << "x" << cols << std::endl;
prof.toc("read");
// The number of unknowns in the U subsystem
ptrdiff_t nu = std::stoi(argv[3]);
// We use the tuple of CRS arrays to represent the system matrix.
// Note that std::tie creates a tuple of references, so no data is actually
// copied here:
auto A = std::tie(rows, ptr, col, val);
// Compose the solver type
typedef amgcl::backend::builtin<double> SBackend; // the outer iterative solver backend
typedef amgcl::backend::builtin<float> PBackend; // the PSolver backend
typedef amgcl::backend::builtin<
amgcl::static_matrix<float,3,3>> UBackend; // the USolver backend
typedef amgcl::make_solver<
amgcl::preconditioner::schur_pressure_correction<
amgcl::make_block_solver<
amgcl::amg<
UBackend,
amgcl::coarsening::aggregation,
amgcl::relaxation::ilu0
>,
amgcl::solver::preonly<UBackend>
>,
amgcl::make_solver<
amgcl::relaxation::as_preconditioner<
PBackend,
amgcl::relaxation::spai0
>,
amgcl::solver::preonly<PBackend>
>
>,
amgcl::solver::cg<SBackend>
> Solver;
// Solver parameters
Solver::params prm;
prm.precond.simplec_dia = false;
prm.precond.pmask.resize(rows);
for(ptrdiff_t i = 0; i < rows; ++i) prm.precond.pmask[i] = (i >= nu);
// Initialize the solver with the system matrix.
prof.tic("setup");
Solver solve(A, prm);
prof.toc("setup");
// Show the mini-report on the constructed solver:
std::cout << solve << std::endl;
// Solve the system with the zero initial approximation:
int iters;
double error;
std::vector<double> x(rows, 0.0);
prof.tic("solve");
std::tie(iters, error) = solve(A, rhs, x);
prof.toc("solve");
// Output the number of iterations, the relative error,
// and the profiling data:
std::cout << "Iters: " << iters << std::endl
<< "Error: " << error << std::endl
<< prof << std::endl;
}
|
Schur pressure correction is composite preconditioner. Its definition includes definition of two nested iterative solvers, one for the “flow” (U) subsystem, and the other for the “pressure” (P) subsystem. In lines 55–58 we define the backends used in the outer iterative solver, and in the two nested solvers. Note that both backends for nested solvers use single precision values, and the flow subsystem backend has block value type:
55 56 57 58 | typedef amgcl::backend::builtin<double> SBackend; // the outer iterative solver backend
typedef amgcl::backend::builtin<float> PBackend; // the PSolver backend
typedef amgcl::backend::builtin<
amgcl::static_matrix<float,3,3>> UBackend; // the USolver backend
|
In lines 60-79 we define the solver type. The flow solver is defined in lines
62-69, and the pressure solver – in lines 70–77. Both are using
amgcl::solver::preonly as “iterative” solver, which in fact only
applies the specified preconditioner once. The flow solver is defined with
amgcl::make_block_solver, which automatically converts its
input matrix \(A\) to the block format during the setup and reinterprets
the scalar RHS and solution vectors as having block values during solution:
60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | typedef amgcl::make_solver<
amgcl::preconditioner::schur_pressure_correction<
amgcl::make_block_solver<
amgcl::amg<
UBackend,
amgcl::coarsening::aggregation,
amgcl::relaxation::ilu0
>,
amgcl::solver::preonly<UBackend>
>,
amgcl::make_solver<
amgcl::relaxation::as_preconditioner<
PBackend,
amgcl::relaxation::spai0
>,
amgcl::solver::preonly<PBackend>
>
>,
amgcl::solver::cg<SBackend>
> Solver;
|
In the solver parameters we disable lumping of the matrix \(A\) diagonal for the Schur complement approimation (line 83) and fill the pressure mask to indicate which unknowns correspond to the pressure subsystem (lines 84–85):
81 82 83 84 85 | // Solver parameters
Solver::params prm;
prm.precond.simplec_dia = false;
prm.precond.pmask.resize(rows);
for(ptrdiff_t i = 0; i < rows; ++i) prm.precond.pmask[i] = (i >= nu);
|
Here is the output from the compiled program. The preconditioner uses 398M or memory, as opposed to 587M in the case of the full precision preconditioner used in the examples/schur_pressure_correction, and both the setup and the solution are about 50% faster due to the use of the mixed precision approach:
$ ./stokes_ucube ucube_4_A.bin ucube_4_b.bin 456192
Matrix ucube_4_A.bin: 554496x554496
RHS ucube_4_b.bin: 554496x1
Solver
======
Type: CG
Unknowns: 554496
Memory footprint: 16.92 M
Preconditioner
==============
Schur complement (two-stage preconditioner)
Unknowns: 554496(98304)
Nonzeros: 14292884
Memory: 398.39 M
[ U ]
Solver
======
Type: PreOnly
Unknowns: 152064
Memory footprint: 0.00 B
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.25
Grid complexity: 1.14
Memory footprint: 130.49 M
level unknowns nonzeros memory
---------------------------------------------
0 152064 982416 105.64 M (80.25%)
1 18654 197826 19.56 M (16.16%)
2 2619 35991 3.44 M ( 2.94%)
3 591 7953 1.85 M ( 0.65%)
[ P ]
Solver
======
Type: PreOnly
Unknowns: 98304
Memory footprint: 0.00 B
Preconditioner
==============
Relaxation as preconditioner
Unknowns: 98304
Nonzeros: 274472
Memory: 4.27 M
Iters: 35
Error: 8.57996e-09
[UCube4: 2.502 s] (100.00%)
[ read: 0.129 s] ( 5.16%)
[ setup: 0.240 s] ( 9.57%)
[ solve: 2.132 s] ( 85.19%)
Converting the solver to the VexCL backend in order to accelerate the solution with GPGPU is straightforward. Below is the complete source code of the solver (tutorial/4.Stokes/stokes_ucube_vexcl.cpp), with the differences between the OpenMP and the VexCL versions highlighted. Note that the GPU version of the ILU(0) smoother approximates the lower and upper triangular solves in the incomplete LU decomposition with a couple of Jacobi iterations [ChPa15]. Here we set the number of iterations to 4 (line 94).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 | #include <iostream>
#include <string>
#include <amgcl/backend/vexcl.hpp>
#include <amgcl/backend/vexcl_static_matrix.hpp>
#include <amgcl/adapter/crs_tuple.hpp>
#include <amgcl/value_type/static_matrix.hpp>
#include <amgcl/adapter/block_matrix.hpp>
#include <amgcl/preconditioner/schur_pressure_correction.hpp>
#include <amgcl/make_solver.hpp>
#include <amgcl/make_block_solver.hpp>
#include <amgcl/amg.hpp>
#include <amgcl/solver/cg.hpp>
#include <amgcl/solver/preonly.hpp>
#include <amgcl/coarsening/aggregation.hpp>
#include <amgcl/relaxation/ilu0.hpp>
#include <amgcl/relaxation/spai0.hpp>
#include <amgcl/relaxation/as_preconditioner.hpp>
#include <amgcl/io/binary.hpp>
#include <amgcl/profiler.hpp>
//---------------------------------------------------------------------------
int main(int argc, char *argv[]) {
// The command line should contain the matrix and the RHS file names,
// and the number of unknowns in the flow subsytem:
if (argc < 4) {
std::cerr << "Usage: " << argv[0] << " <matrix.bin> <rhs.bin> <nu>" << std::endl;
return 1;
}
// Create VexCL context. Set the environment variable OCL_DEVICE to
// control which GPU to use in case multiple are available,
// and use single device:
vex::Context ctx(vex::Filter::Env && vex::Filter::Count(1));
std::cout << ctx << std::endl;
// Enable support for block-valued matrices in the VexCL kernels:
vex::scoped_program_header header(ctx, amgcl::backend::vexcl_static_matrix_declaration<float,3>());
// The profiler:
amgcl::profiler<> prof("UCube4 (VexCL)");
// Read the system matrix:
ptrdiff_t rows, cols;
std::vector<ptrdiff_t> ptr, col;
std::vector<double> val, rhs;
prof.tic("read");
amgcl::io::read_crs(argv[1], rows, ptr, col, val);
amgcl::io::read_dense(argv[2], rows, cols, rhs);
std::cout << "Matrix " << argv[1] << ": " << rows << "x" << rows << std::endl;
std::cout << "RHS " << argv[2] << ": " << rows << "x" << cols << std::endl;
prof.toc("read");
// The number of unknowns in the U subsystem
ptrdiff_t nu = std::stoi(argv[3]);
// We use the tuple of CRS arrays to represent the system matrix.
// Note that std::tie creates a tuple of references, so no data is actually
// copied here:
auto A = std::tie(rows, ptr, col, val);
// Compose the solver type
typedef amgcl::backend::vexcl<double> SBackend; // the outer iterative solver backend
typedef amgcl::backend::vexcl<float> PBackend; // the PSolver backend
typedef amgcl::backend::vexcl<
amgcl::static_matrix<float,3,3>> UBackend; // the USolver backend
typedef amgcl::make_solver<
amgcl::preconditioner::schur_pressure_correction<
amgcl::make_block_solver<
amgcl::amg<
UBackend,
amgcl::coarsening::aggregation,
amgcl::relaxation::ilu0
>,
amgcl::solver::preonly<UBackend>
>,
amgcl::make_solver<
amgcl::relaxation::as_preconditioner<
PBackend,
amgcl::relaxation::spai0
>,
amgcl::solver::preonly<PBackend>
>
>,
amgcl::solver::cg<SBackend>
> Solver;
// Solver parameters
Solver::params prm;
prm.precond.simplec_dia = false;
prm.precond.usolver.precond.relax.solve.iters = 4;
prm.precond.pmask.resize(rows);
for(ptrdiff_t i = 0; i < rows; ++i) prm.precond.pmask[i] = (i >= nu);
// Set the VexCL context in the backend parameters
SBackend::params bprm;
bprm.q = ctx;
// Initialize the solver with the system matrix.
prof.tic("setup");
Solver solve(A, prm, bprm);
prof.toc("setup");
// Show the mini-report on the constructed solver:
std::cout << solve << std::endl;
// Since we are using mixed precision, we have to transfer the system matrix to the GPU:
prof.tic("GPU matrix");
auto A_gpu = SBackend::copy_matrix(std::make_shared<amgcl::backend::crs<double>>(A), bprm);
prof.toc("GPU matrix");
// Solve the system with the zero initial approximation:
int iters;
double error;
vex::vector<double> f(ctx, rhs);
vex::vector<double> x(ctx, rows);
x = 0.0;
prof.tic("solve");
std::tie(iters, error) = solve(*A_gpu, f, x);
prof.toc("solve");
// Output the number of iterations, the relative error,
// and the profiling data:
std::cout << "Iters: " << iters << std::endl
<< "Error: " << error << std::endl
<< prof << std::endl;
}
|
The output of the VexCL version is shown below. The solution phase is about twice as fast as the OpenMP version:
$ ./stokes_ucube_vexcl_cuda ucube_4_A.bin ucube_4_b.bin 456192
1. GeForce GTX 1050 Ti
Matrix ucube_4_A.bin: 554496x554496
RHS ucube_4_b.bin: 554496x1
Solver
======
Type: CG
Unknowns: 554496
Memory footprint: 16.92 M
Preconditioner
==============
Schur complement (two-stage preconditioner)
Unknowns: 554496(98304)
Nonzeros: 14292884
Memory: 399.66 M
[ U ]
Solver
======
Type: PreOnly
Unknowns: 152064
Memory footprint: 0.00 B
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.25
Grid complexity: 1.14
Memory footprint: 131.76 M
level unknowns nonzeros memory
---------------------------------------------
0 152064 982416 106.76 M (80.25%)
1 18654 197826 19.68 M (16.16%)
2 2619 35991 3.45 M ( 2.94%)
3 591 7953 1.86 M ( 0.65%)
[ P ]
Solver
======
Type: PreOnly
Unknowns: 98304
Memory footprint: 0.00 B
Preconditioner
==============
Relaxation as preconditioner
Unknowns: 98304
Nonzeros: 274472
Memory: 4.27 M
Iters: 36
Error: 7.26253e-09
[UCube4 (VexCL): 1.858 s] (100.00%)
[ self: 0.004 s] ( 0.20%)
[ GPU matrix: 0.213 s] ( 11.46%)
[ read: 0.128 s] ( 6.87%)
[ setup: 0.519 s] ( 27.96%)
[ solve: 0.994 s] ( 53.52%)