Structural problem¶
This system may be downloaded from the Serena page (use the Matrix Market download option). According to the description, the system represents a 3D gas resevoir simulation for CO2 sequestration, and was obtained from a structural problem discretizing a gas reservoir with tetrahedral Finite Elements. The medium is strongly heterogeneous and characterized by a complex geometry consisting of alternating sequences of thin clay and sand layers. More details available in [FGJT10]. Note that the RHS vector for the Serena problem is not provided, and we use the RHS vector filled with ones.
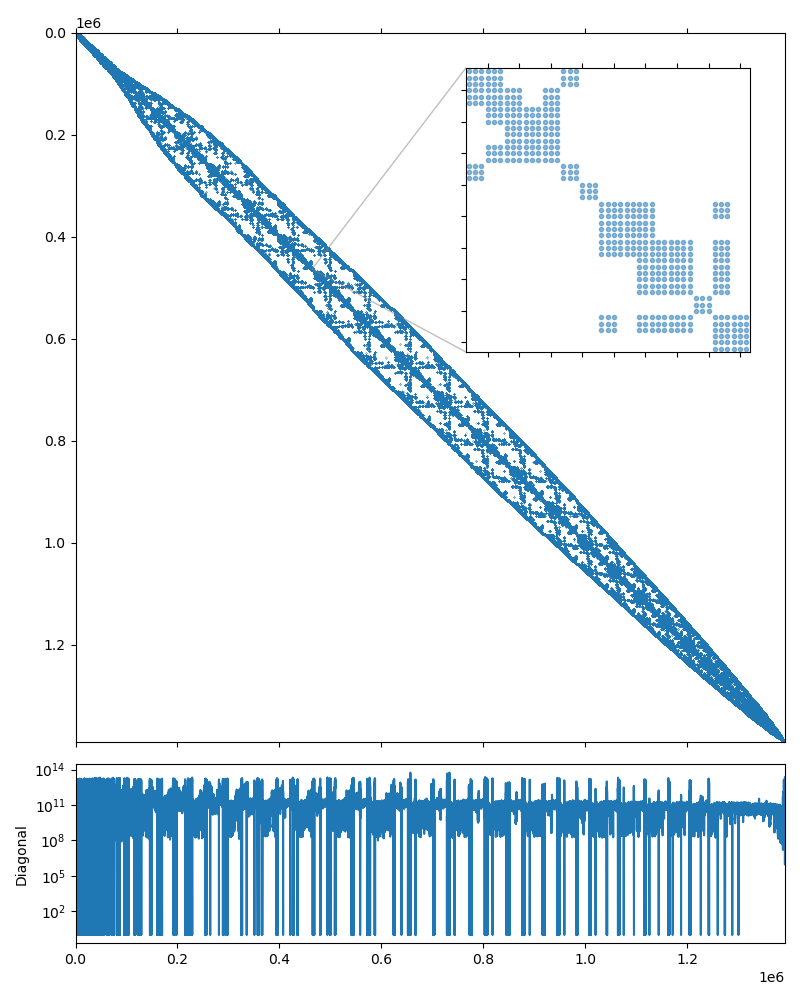
The system matrix is symmetric, and has 1,391,349 rows and 64,131,971 nonzero values, which corresponds to an average of 46 nonzeros per row. The matrix portrait is shown on the figure below.
| [FGJT10] |
|
As in the case of Poisson problem tutorial, we start experimenting with the examples/solver utility provided by AMGCL. The default options do not seem to work this time. The relative error did not reach the required threshold of 1e-8 and the solver exited after the default limit of 100 iterations:
$ solver -A Serena.mtx
Solver
======
Type: BiCGStab
Unknowns: 1391349
Memory footprint: 74.31 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.22
Grid complexity: 1.08
Memory footprint: 1.45 G
level unknowns nonzeros memory
---------------------------------------------
0 1391349 64531701 1.22 G (82.01%)
1 98824 13083884 218.40 M (16.63%)
2 5721 1038749 16.82 M ( 1.32%)
3 279 29151 490.75 K ( 0.04%)
Iterations: 100
Error: 0.000874761
[Profile: 74.102 s] (100.00%)
[ reading: 18.505 s] ( 24.97%)
[ setup: 2.101 s] ( 2.84%)
[ solve: 53.489 s] ( 72.18%)
The system is quite large and just reading from the text-based Matrix Market format takes 18.5 seconds. No one has that amount of free time on their hands, so lets convert the matrix into the binary format with the examples/mm2bin utility. This should make the experiments slightly less painful:
mm2bin -i Serena.mtx -o Serena.bin
Wrote 1391349 by 1391349 sparse matrix, 64531701 nonzeros
The -B option tells the solver that the input is in
binary format now. Lets also increase the maximum iteration limit this time to
see if the solver manages to converge at all:
$ solver -B -A Serena.bin solver.maxiter=1000
Solver
======
Type: BiCGStab
Unknowns: 1391349
Memory footprint: 74.31 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.22
Grid complexity: 1.08
Memory footprint: 1.45 G
level unknowns nonzeros memory
---------------------------------------------
0 1391349 64531701 1.22 G (82.01%)
1 98824 13083884 218.40 M (16.63%)
2 5721 1038749 16.82 M ( 1.32%)
3 279 29151 490.75 K ( 0.04%)
Iterations: 211
Error: 8.54558e-09
[Profile: 114.703 s] (100.00%)
[ reading: 0.550 s] ( 0.48%)
[ setup: 2.114 s] ( 1.84%)
[ solve: 112.034 s] ( 97.67%)
The input matrix is read much faster now, and the solver does converge, but the
convergence rate is not great. Looking closer at the Serena matrix portrait figure,
the matrix seems to have block structure with \(3\times3\) blocks. This is
usually the case when the system has been obtained via discretization of a
system of coupled PDEs, or has vector unknowns. We have to guess here, but
since the problem is described as “structural”, then each block probably
corresponds to the 3D displacement vector of a single grid node. We can
communicate this piece of information to AMGCL using the block_size
parameter of the aggregation method:
$ solver -B -A Serena.bin solver.maxiter=1000 \
precond.coarsening.aggr.block_size=3
Solver
======
Type: BiCGStab
Unknowns: 1391349
Memory footprint: 74.31 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.31
Grid complexity: 1.08
Memory footprint: 1.84 G
level unknowns nonzeros memory
---------------------------------------------
0 1391349 64531701 1.50 G (76.48%)
1 109764 17969220 316.66 M (21.30%)
2 6291 1788507 29.51 M ( 2.12%)
3 429 82719 1.23 M ( 0.10%)
Iterations: 120
Error: 9.73074e-09
[Profile: 73.296 s] (100.00%)
[ reading: 0.587 s] ( 0.80%)
[ setup: 2.709 s] ( 3.70%)
[ solve: 69.994 s] ( 95.49%)
This has definitely improved the convergence! We also know that the matrix is symmetric, so lets switch the solver from the default BiCGStab to the slightly less expensive CG:
$ solver -B -A Serena.bin \
solver.type=cg \
solver.maxiter=1000 \
precond.coarsening.aggr.block_size=3
Solver
======
Type: CG
Unknowns: 1391349
Memory footprint: 42.46 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.31
Grid complexity: 1.08
Memory footprint: 1.84 G
level unknowns nonzeros memory
---------------------------------------------
0 1391349 64531701 1.50 G (76.48%)
1 109764 17969220 316.66 M (21.30%)
2 6291 1788507 29.51 M ( 2.12%)
3 429 82719 1.23 M ( 0.10%)
Iterations: 177
Error: 8.6598e-09
[Profile: 55.250 s] (100.00%)
[ reading: 0.550 s] ( 1.00%)
[ setup: 2.801 s] ( 5.07%)
[ solve: 51.894 s] ( 93.92%)
This reduces the solution time, even though the number of iterations has grown. Each iteration of BiCGStab costs about twice as much as a CG iteration, because BiCGStab does two matrix-vector products and preconditioner applications per iteration, while CG only does one.
The problem description states that the medium is strongly heterogeneous and
characterized by a complex geometry consisting of alternating sequences of thin
clay and sand layers. This may result in high contrast between matrix
coefficients in the neighboring rows, which is confirmed by the plot of the
matrix diagonal in Serena matrix portrait: the diagonal coefficients span more than
10 orders of magnitude! Scaling the matrix (so that it has the unit diagonal)
should help with the convergence. The -s option tells the solver to do
that:
$ solver -B -A Serena.bin -s \
solver.type=cg solver.maxiter=200 \
precond.coarsening.aggr.block_size=3
Solver
======
Type: CG
Unknowns: 1391349
Memory footprint: 42.46 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.29
Grid complexity: 1.08
Memory footprint: 1.82 G
level unknowns nonzeros memory
---------------------------------------------
0 1391349 64531701 1.51 G (77.81%)
1 100635 16771185 294.81 M (20.22%)
2 5643 1571157 25.92 M ( 1.89%)
3 342 60264 802.69 K ( 0.07%)
Iterations: 112
Error: 9.84457e-09
[Profile: 36.021 s] (100.00%)
[ self: 0.204 s] ( 0.57%)
[ reading: 0.564 s] ( 1.57%)
[ setup: 2.684 s] ( 7.45%)
[ solve: 32.568 s] ( 90.42%)
And the convergence has indeed been improved! Finally, when the matrix has
block structure, as in this case, it often pays to use the block-valued
backend, so that the system matrix has three times fewer rows and columns, but
each nonzero entry is a statically sized \(3\times3\) matrix. This should
be done instead of specifying the block_size aggregation parameter, as the
aggregation now naturally operates with the \(3\times3\) blocks:
$ solver -B -A Serena.bin solver.type=cg solver.maxiter=200 -s -b3
Solver
======
Type: CG
Unknowns: 463783
Memory footprint: 42.46 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.27
Grid complexity: 1.08
Memory footprint: 1.04 G
level unknowns nonzeros memory
---------------------------------------------
0 463783 7170189 891.53 M (78.80%)
1 33052 1772434 159.22 M (19.48%)
2 1722 151034 12.72 M ( 1.66%)
3 98 5756 612.72 K ( 0.06%)
Iterations: 162
Error: 9.7497e-09
[Profile: 31.122 s] (100.00%)
[ self: 0.204 s] ( 0.66%)
[ reading: 0.550 s] ( 1.77%)
[ setup: 1.013 s] ( 3.26%)
[ solve: 29.354 s] ( 94.32%)
Note that the preconditioner now requires 1.04G of memory as opposed to 1.82G in the scalar case. The setup is about 2.5 times faster, and the solution phase performance has been slightly improved, even though the number of iteration has grown. This is explained by the fact that the matrix is now symbolically smaller, and is easier to analyze during setup. The matrix also occupies less memory for the CRS arrays, and is more cache-friendly, which helps to speed up the solution phase. This seems to be the best we can get with this system, so let us implement this version. We will also use the mixed precision approach in order to get as much performance as possible from the solution. The listing below shows the complete solution and is also available in tutorial/2.Serena/serena.cpp.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 | #include <vector>
#include <iostream>
#include <amgcl/backend/builtin.hpp>
#include <amgcl/adapter/crs_tuple.hpp>
#include <amgcl/make_solver.hpp>
#include <amgcl/amg.hpp>
#include <amgcl/coarsening/smoothed_aggregation.hpp>
#include <amgcl/relaxation/spai0.hpp>
#include <amgcl/solver/cg.hpp>
#include <amgcl/value_type/static_matrix.hpp>
#include <amgcl/adapter/block_matrix.hpp>
#include <amgcl/io/mm.hpp>
#include <amgcl/profiler.hpp>
int main(int argc, char *argv[]) {
// The command line should contain the matrix file name:
if (argc < 2) {
std::cerr << "Usage: " << argv[0] << " <matrix.mtx>" << std::endl;
return 1;
}
// The profiler:
amgcl::profiler<> prof("Serena");
// Read the system matrix:
ptrdiff_t rows, cols;
std::vector<ptrdiff_t> ptr, col;
std::vector<double> val;
prof.tic("read");
std::tie(rows, cols) = amgcl::io::mm_reader(argv[1])(ptr, col, val);
std::cout << "Matrix " << argv[1] << ": " << rows << "x" << cols << std::endl;
prof.toc("read");
// The RHS is filled with ones:
std::vector<double> f(rows, 1.0);
// Scale the matrix so that it has the unit diagonal.
// First, find the diagonal values:
std::vector<double> D(rows, 1.0);
for(ptrdiff_t i = 0; i < rows; ++i) {
for(ptrdiff_t j = ptr[i], e = ptr[i+1]; j < e; ++j) {
if (col[j] == i) {
D[i] = 1 / sqrt(val[j]);
break;
}
}
}
// Then, apply the scaling in-place:
for(ptrdiff_t i = 0; i < rows; ++i) {
for(ptrdiff_t j = ptr[i], e = ptr[i+1]; j < e; ++j) {
val[j] *= D[i] * D[col[j]];
}
f[i] *= D[i];
}
// We use the tuple of CRS arrays to represent the system matrix.
// Note that std::tie creates a tuple of references, so no data is actually
// copied here:
auto A = std::tie(rows, ptr, col, val);
// Compose the solver type
typedef amgcl::static_matrix<double, 3, 3> dmat_type; // matrix value type in double precision
typedef amgcl::static_matrix<double, 3, 1> dvec_type; // the corresponding vector value type
typedef amgcl::static_matrix<float, 3, 3> smat_type; // matrix value type in single precision
typedef amgcl::backend::builtin<dmat_type> SBackend; // the solver backend
typedef amgcl::backend::builtin<smat_type> PBackend; // the preconditioner backend
typedef amgcl::make_solver<
amgcl::amg<
PBackend,
amgcl::coarsening::smoothed_aggregation,
amgcl::relaxation::spai0
>,
amgcl::solver::cg<SBackend>
> Solver;
// Solver parameters
Solver::params prm;
prm.solver.maxiter = 500;
// Initialize the solver with the system matrix.
// Use the block_matrix adapter to convert the matrix into
// the block format on the fly:
prof.tic("setup");
auto Ab = amgcl::adapter::block_matrix<dmat_type>(A);
Solver solve(Ab, prm);
prof.toc("setup");
// Show the mini-report on the constructed solver:
std::cout << solve << std::endl;
// Solve the system with the zero initial approximation:
int iters;
double error;
std::vector<double> x(rows, 0.0);
// Reinterpret both the RHS and the solution vectors as block-valued:
auto f_ptr = reinterpret_cast<dvec_type*>(f.data());
auto x_ptr = reinterpret_cast<dvec_type*>(x.data());
auto F = amgcl::make_iterator_range(f_ptr, f_ptr + rows / 3);
auto X = amgcl::make_iterator_range(x_ptr, x_ptr + rows / 3);
prof.tic("solve");
std::tie(iters, error) = solve(Ab, F, X);
prof.toc("solve");
// Output the number of iterations, the relative error,
// and the profiling data:
std::cout << "Iters: " << iters << std::endl
<< "Error: " << error << std::endl
<< prof << std::endl;
}
|
In addition the the includes described in Poisson problem, we also include
the headers for the amgcl::static_matrix value type, and the
amgcl::adapter::block_matrix() adapter that transparently converts
a scalar matrix to the block format. In lines 42–58 we apply the scaling
according to the following formula:
where \(A_s\) and \(f_s\) are the scaled matrix and the RHS vector, and \(D\) is the diagonal of the matrix \(A\). After solving the scaled system \(A_s y = f_s\), the solution to the original system may be found as \(x = D^{-1/2} y\).
In lines 66–68 we define the block value types for the matrix and the RHS and
solution vectors. dmat_type and smat_type are \(3\times3\) static
matrices used as value types with the double precision solver backend and the
single precision preconditioner backend. dvec_type is a double precision
\(3\times1\) matrix (or a vector) used as a value type for the RHS and the
solution.
The solver class definition in lines 73–80 is almost the same as in the Poisson problem case, with the exception that we are using the CG iterative solver this time. In lines 83–84 we define the solver parameters. Namely, we increase the maximum iterations limit to 500 iterations.
In lines 90–91 we instantiate the solver, using the block_matrix adapter
in order to convert the scalar matrix into the block format. The adapter
operates on a row-by-row basis and does not create a temporary copy of the
matrix.
In lines 103–106 we convert the scalar RHS and solution vectors to the
block-valued ones. We use the fact that 3 consecutive elements of a scalar
array may be reinterpreted as a single \(3\times1\) static matrix. Using
the reinterpret_cast trick we can get the block-valued view into the RHS
and the solution vectors data without extra memory copies.
Here is the output of the program:
$ ./serena Serena.mtx
Matrix Serena.mtx: 1391349x1391349
Solver
======
Type: CG
Unknowns: 463783
Memory footprint: 42.46 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.27
Grid complexity: 1.08
Memory footprint: 585.33 M
level unknowns nonzeros memory
---------------------------------------------
0 463783 7170189 490.45 M (78.80%)
1 33052 1772434 87.58 M (19.48%)
2 1722 151034 7.00 M ( 1.66%)
3 98 5756 306.75 K ( 0.06%)
Iters: 162
Error: 9.74929e-09
[Serena: 48.427 s] (100.00%)
[ self: 0.166 s] ( 0.34%)
[ read: 21.115 s] ( 43.60%)
[ setup: 0.749 s] ( 1.55%)
[ solve: 26.397 s] ( 54.51%)
Note that due to the use of mixed precision the preconditioner consumes 585.33M of memory as opposed to 1.08G from the example above. The setup and the solution are faster that the full precision version by about 30% and 10% correspondingly.
Let us see if using a GPU backend may further improve the performance. The CUDA backend does not support block value types, so we will use the VexCL backend (which, in turn, may use either OpenCL, CUDA, or OpenMP). The listing below contains the complete source for the solution (available at tutorial/2.Serena/serena_vexcl.cpp). The differences with the builtin backend version are highlighted.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 | #include <vector>
#include <iostream>
#include <amgcl/backend/vexcl.hpp>
#include <amgcl/backend/vexcl_static_matrix.hpp>
#include <amgcl/adapter/crs_tuple.hpp>
#include <amgcl/make_solver.hpp>
#include <amgcl/amg.hpp>
#include <amgcl/coarsening/smoothed_aggregation.hpp>
#include <amgcl/relaxation/spai0.hpp>
#include <amgcl/solver/cg.hpp>
#include <amgcl/value_type/static_matrix.hpp>
#include <amgcl/adapter/block_matrix.hpp>
#include <amgcl/io/mm.hpp>
#include <amgcl/profiler.hpp>
int main(int argc, char *argv[]) {
// The command line should contain the matrix file name:
if (argc < 2) {
std::cerr << "Usage: " << argv[0] << " <matrix.mtx>" << std::endl;
return 1;
}
// Create VexCL context. Set the environment variable OCL_DEVICE to
// control which GPU to use in case multiple are available,
// and use single device:
vex::Context ctx(vex::Filter::Env && vex::Filter::Count(1));
std::cout << ctx << std::endl;
// Enable support for block-valued matrices in the VexCL kernels:
vex::scoped_program_header h1(ctx, amgcl::backend::vexcl_static_matrix_declaration<double,3>());
vex::scoped_program_header h2(ctx, amgcl::backend::vexcl_static_matrix_declaration<float,3>());
// The profiler:
amgcl::profiler<> prof("Serena (VexCL)");
// Read the system matrix:
ptrdiff_t rows, cols;
std::vector<ptrdiff_t> ptr, col;
std::vector<double> val;
prof.tic("read");
std::tie(rows, cols) = amgcl::io::mm_reader(argv[1])(ptr, col, val);
std::cout << "Matrix " << argv[1] << ": " << rows << "x" << cols << std::endl;
prof.toc("read");
// The RHS is filled with ones:
std::vector<double> f(rows, 1.0);
// Scale the matrix so that it has the unit diagonal.
// First, find the diagonal values:
std::vector<double> D(rows, 1.0);
for(ptrdiff_t i = 0; i < rows; ++i) {
for(ptrdiff_t j = ptr[i], e = ptr[i+1]; j < e; ++j) {
if (col[j] == i) {
D[i] = 1 / sqrt(val[j]);
break;
}
}
}
// Then, apply the scaling in-place:
for(ptrdiff_t i = 0; i < rows; ++i) {
for(ptrdiff_t j = ptr[i], e = ptr[i+1]; j < e; ++j) {
val[j] *= D[i] * D[col[j]];
}
f[i] *= D[i];
}
// We use the tuple of CRS arrays to represent the system matrix.
// Note that std::tie creates a tuple of references, so no data is actually
// copied here:
auto A = std::tie(rows, ptr, col, val);
// Compose the solver type
typedef amgcl::static_matrix<double, 3, 3> dmat_type; // matrix value type in double precision
typedef amgcl::static_matrix<double, 3, 1> dvec_type; // the corresponding vector value type
typedef amgcl::static_matrix<float, 3, 3> smat_type; // matrix value type in single precision
typedef amgcl::backend::vexcl<dmat_type> SBackend; // the solver backend
typedef amgcl::backend::vexcl<smat_type> PBackend; // the preconditioner backend
typedef amgcl::make_solver<
amgcl::amg<
PBackend,
amgcl::coarsening::smoothed_aggregation,
amgcl::relaxation::spai0
>,
amgcl::solver::cg<SBackend>
> Solver;
// Solver parameters
Solver::params prm;
prm.solver.maxiter = 500;
// Set the VexCL context in the backend parameters
SBackend::params bprm;
bprm.q = ctx;
// Initialize the solver with the system matrix.
// We use the block_matrix adapter to convert the matrix into the block
// format on the fly:
prof.tic("setup");
auto Ab = amgcl::adapter::block_matrix<dmat_type>(A);
Solver solve(Ab, prm, bprm);
prof.toc("setup");
// Show the mini-report on the constructed solver:
std::cout << solve << std::endl;
// Solve the system with the zero initial approximation:
int iters;
double error;
std::vector<double> x(rows, 0.0);
// Since we are using mixed precision, we have to transfer the system matrix to the GPU:
prof.tic("GPU matrix");
auto A_gpu = SBackend::copy_matrix(
std::make_shared<amgcl::backend::crs<dmat_type>>(Ab), bprm);
prof.toc("GPU matrix");
// We reinterpret both the RHS and the solution vectors as block-valued,
// and copy them to the VexCL vectors:
auto f_ptr = reinterpret_cast<dvec_type*>(f.data());
auto x_ptr = reinterpret_cast<dvec_type*>(x.data());
vex::vector<dvec_type> F(ctx, rows / 3, f_ptr);
vex::vector<dvec_type> X(ctx, rows / 3, x_ptr);
prof.tic("solve");
std::tie(iters, error) = solve(*A_gpu, F, X);
prof.toc("solve");
// Output the number of iterations, the relative error,
// and the profiling data:
std::cout << "Iters: " << iters << std::endl
<< "Error: " << error << std::endl
<< prof << std::endl;
}
|
In the include section, we replace the header for the builtin backend with the one for the VexCL backend, and also include the header with support for block values in VexCL (lines 4–5). In lines 28–29 we initialize the VexCL context, and in lines 32–33 we enable the VexCL support for \(3\times3\) static matrices in both double and single precision.
In lines 81–82 we define the solver and preconditioner backends as VexCL backends with the corresponding matrix value types. In lines 98–99 we reference the VexCL context in the backend parameters.
Since we are using the GPU backend, we have to explicitly form the block valued matrix and transfer it to the GPU. This is done in lines 119–120. In lines 127–128 we copy the RHS and the solution vectors to the GPU, and we solve the system in line 131.
The output of the program is shown below:
$ ./serena_vexcl_cuda Serena.mtx
1. GeForce GTX 1050 Ti
Matrix Serena.mtx: 1391349x1391349
Solver
======
Type: CG
Unknowns: 463783
Memory footprint: 42.46 M
Preconditioner
==============
Number of levels: 4
Operator complexity: 1.27
Grid complexity: 1.08
Memory footprint: 585.33 M
level unknowns nonzeros memory
---------------------------------------------
0 463783 7170189 490.45 M (78.80%)
1 33052 1772434 87.58 M (19.48%)
2 1722 151034 7.00 M ( 1.66%)
3 98 5756 309.04 K ( 0.06%)
Iters: 162
Error: 9.74928e-09
[Serena (VexCL): 27.208 s] (100.00%)
[ self: 0.180 s] ( 0.66%)
[ GPU matrix: 0.604 s] ( 2.22%)
[ read: 18.699 s] ( 68.73%)
[ setup: 1.308 s] ( 4.81%)
[ solve: 6.417 s] ( 23.59%)
The setup time has increased from 0.7 seconds for the builtin backend to 1.3 seconds, and we also see the additional 0.6 seconds for transferring the matrix to the GPU. But the solution time has decreased from 26.4 to 6.4 seconds, which is about 4 times faster.